Hightower’s Algorithm

One of the traditional algorithms of solving routing problems in VLSI Design Automation is Hightower’s Algorithm.

I haven’t seen someone writing about this algorithm on the internet and only see some extremely high-level concept of it on some lecture slides.

Let’s dive into its details and think about the unsolvable conditions.

📄 Source:

📜 Hightower, 1969, A solution to line-routing problems on the continuous plane, DAC 1969.

The Routing Problem

In a 2D map, we have a source and a target point. We want to find a path that connects those 2 points, but there are obstacles on the map.

Previously, Mikami & Tabuchi’s Algorithm can be applied to solve these problems, but it is restricted to grid maps and have a lot of computation overhead.

Hightower’s Algorithm is an enhanced version of Mikami & Tabuchi’s Algorithm, and can work on continuous 2D maps.

Hightower’s Algorithm

Let \(S\), \(T\) be the source and target point.

1. For \(S\) and \(T\) simultaneously, construct a vertical or horizontal escape line where \(S\), \(T\) is an object point.

2. When a new escape line is constructed, an escape point is added under one of the 2 conditions:

   • Just before the line hits an obstacle.
   • Just passing one of the nearest parallel obstacle line segments.

   The escape points are found by moving a unit away from the object point, along the line. The process stops if an escape point is found, or meeting a previously created escape point. (The new escape point won’t cross an old escape point to avoid falling into an infinite loop)

3. When a new escape point is found, set that escape point to be the new object point.

4. If no escape point is found, that means there exists a previously created escape point on the line. Set the escape point to be one unit nearer the object point starting from the previously created escape point. If there are no such points, exit and report no route found.

5. Repeat until one of \(S\)’s escape line meets one of \(T\)’s escape line.

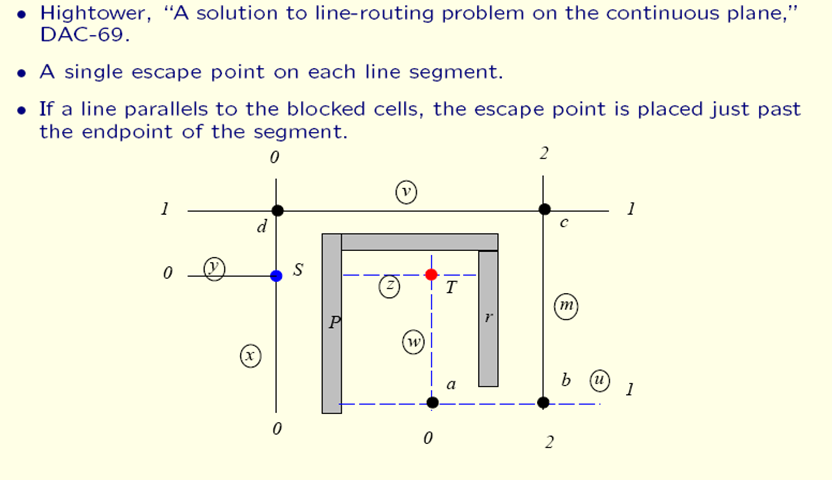
Photo Credit: Prof. David Pan, Lecture 18. Global Routing (II)

Counterexample

The algorithm does not use the same escape line more than once. This means that if the algorithm used an escape line to get into a box that had a very narrow opening, it could not get out again. – Hightower, 1969

If the unit is infinitely small, the algorithm won’t fail to find an existing path.

But since discretizing the 2D map is necessary for practical uses, we can construct counterexamples that illustrates that how can Hightower’s Algorithm fail to find an existing path.

A visualization of the counterexample mentioned in the conclusion of the original paper can be seen as:

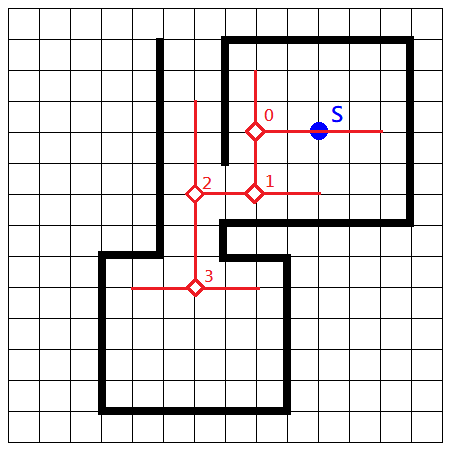
The same structure should be used for both the source \(S\) and the target \(T\), while ensuring there exists a route between them. Since the Point-3 in the image blocks the only exit of the box and the unit size isn’t small enough for other escape lines to go past it, Hightower’s algorithm fails and cannot find an existing route in this map.

✏️ Author’s Note

This issue is a trade off between efficiency and accuracy. The unit size should be chosen depending on the size of the map and available computation resources.